非階層クラスター(k-umeyama)
k-umeyamaとは
k-umeyamaとは、非階層型クラスター分析の圧倒的な精度向上を達成する、クラスター分析の独自手法です。開発者である株式会社クロス・マーケティング在籍梅山貴彦の名をとって「k-umeyama」と名付けました。「k-umeyama」の採用により、マーケティングや広告業界にとどまらず、クラスター分析が日常的に活用されている、画像処理やAIを用いた判断処理等、多くの分野で革新的な精度向上が実現可能となりました。
k-umeyamaは、相関性を排除する因子分析や主成分分析などのデータ加工を介さずに、全てのデータ同士の関係性を加味してクラスタリングをおこないます。結果として、クラスター間は適切に離れ、かつクラスター内のデータは密度が高い状態となる、精度の高い分類を可能にしました。また、シグモイド関数を利用して、的確にクラスター中心を選択するため、外れ値をクラスター中心に選ぶリスクを減らし、クラスター分類の再現性を向上させます。
標準的な非階層型クラスター分析の抱える課題
k-meansのアルゴリズムは、初期シードの選び方に依存して結果が変わり、そのシードが近くに偏ると、クラスタリングの質が低下する可能性が指摘されています。また、ランダムな選択方法により、再現性が低いという課題があります。下記の左側がk-meansのグラフとなりますが、初期シードが1回目と2回目では違う場所が指定され安定性が低いことがわかります。
これらの問題点を解決するための新しいアプローチとして、k-means++が開発されました。この方法では、初期シードを順番に選び出し、前のシードから距離が遠い次のシードを確率的に選択することで、クラスターが均等に分布するように配置されます。この改良により、クラスタリングの質と再現性が向上しました。中央がk-means++、右側がk-umeyamaとなり、それぞれシードの位置は違いますが。1回目と2回目のシードの位置は安定しています。しかし、k-means++は、シードの選択過程で、最も遠い点の外れ値が選ばれやすくなるという弱点があります。
非階層クラスター分析の距離(左:k-means、中央:k-means++、右:k-umeyama)
| 1回目 |  |
 |
 |
| 2回目 |  |
 |
 |
| k-means | k-means++ | k-umeyama |
シードの選択過程の弱点改良に向けて、シグモイド関数を活用
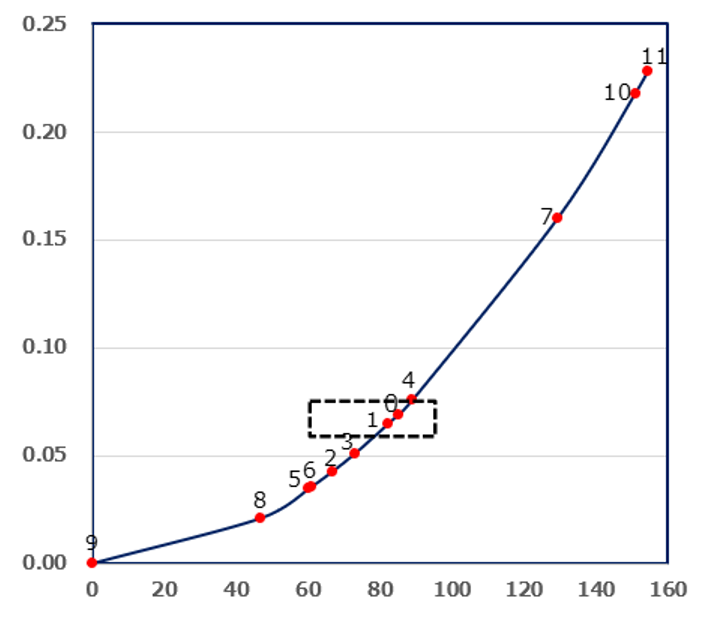
弊社では、k-means++のシード選択に関する課題を解決すべく、新しい手法「k-umeyama」を開発いたしました。この方法は、シグモイド関数を活用することで、各データポイントが距離とウエイト値に基づいて明確に分類される特長があります。具体的な例として、グラフの左側をk-means++、右側をk-umeyamaとして表示した際、k-umeyamaによりデータポイント1や0を比較すると、ウエイトがk-means++(1=0.065,0=0.069)、k-umeyama(1=0.03,0=0.195)とはっきりとした分類となることが確認できます。この技術により、k-means++のシード選択の精度を一層向上させることが期待できます。
シード選択の過程(左:k-means++、右:k-umeyama)
k-means++
k-umeyama
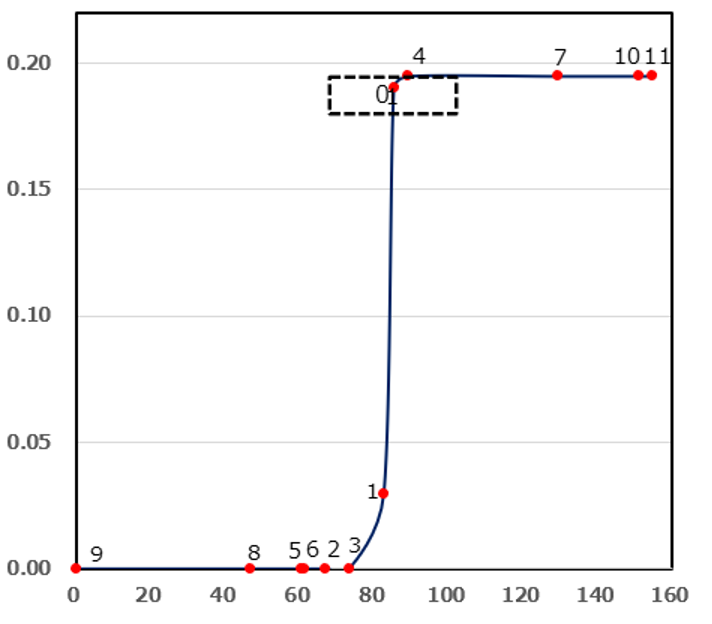
従来の非階層クラスター分析と距離の弱点改良に向けて
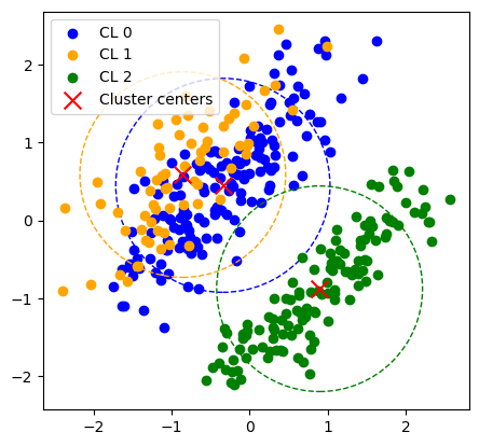
クラスター分析は、似た特徴を持つもの同士をグループにまとめる手法で、特にマーケティング・リサーチの業界でよく用いられます。一般的な手法、k-meansでは、最初にデータを「因子分析・直交化」という方法で整理します。これは、いろいろな情報を簡潔に表すためのステップですが、実は弱点があります。因子分析・直交化はデータの中の関連性を取り除く手法ですが、すべての集団が完璧に相関性を取り除いて整理されているわけではありません。また、因子分析・直交化をおこなうと、データ全体を表現する量が減少することもあります。グラフを用いて、因子分析・直交化したk-meansとマハラノビス汎距離を導入したk-umeyamaのクラスター分析の結果を比較したところ、その差異は一目瞭然となりました。グラフの左側は、因子分析による直交化を施したデータをk-meansでクラスタリングした結果です。こちらは、クラスター0と1が近接し、重なり合う正円の形をしていて、異なる集団がうまく分けられていないことを意味します。一方で、右側のグラフはマハラノビス汎距離を採用したk-umeyamaのクラスタリング結果です。こちらは、3つのクラスターが楕円の形状をとりながら、明確に区別されており、それぞれの集団の特性や違いをより精確に捉えることが確認できます。マハラノビス汎距離を導入することで、明らかにクラスタリングの精度と有用性が大きく向上することがわかります。
クラスター分析結果(左:k-means++、右:k-umeyama)
ユークリッド距離による
k-means(因子分析、直交化)
マハラノビスの汎距離の導入
k-umeyama
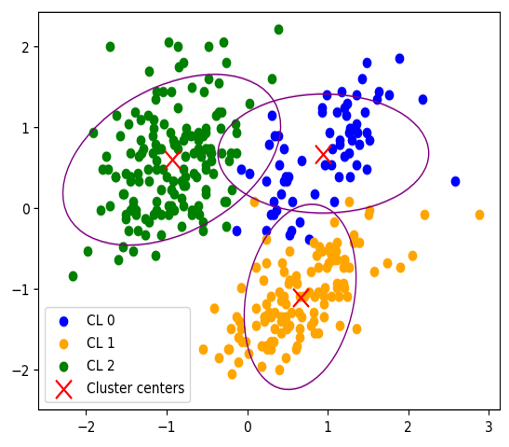
k-umeyamaの計算モデル
ランダムに一つずつ初期シードを選びそのシードと最短距離のdiを選び、すべてのデータポイントを計測、その平均距離を出し、その値をシグモイド関数で変換して、次シードを抽出するためのデータポイントのウエイト付けをします。その後、初回だけユークリッド距離で測り、サンプルをクラスターに所属させます。その後は、クラスター毎に平均と分散共分散、その一般逆行列を算出して、次にマハラノビス距離を測って所属クラスターの更新を繰り返し、クラスターの平均が変化しなくなったら、終了です。
k-umeyamaの計算モデル
| 分析のフロー | 分析内容 |
|---|---|
| ①ランダムに1シードを選択・次のシードを探す |
|
| ②シグモイド関数で変換 |

|
| ③次のシードを抽出する確率のウエイト付け |

|
| ④クラスターの特性を計算 |
|
| ⑤平均からのマハラノビス距離を測ってクラスター所属を更新 ④⇔⑤を繰り返す |

|
| ⑥収束判定・更新・終了 | クラスターの平均値が変化しなくなったら更新を終了 |
精度テスト① 嘴の長さ、深さ等を用いたペンギンの分類
クラスタリングの精度のテストのため、パーマペンギンデータセットを用いて、ペンギンの成鳥の4種類のサイズから「ヒゲペンギン」、「ジェンツーペンギン」、「アデリーペンギン」の3群の正解のあるデータを、k-meansとk-means++、k-umeyamaでクラスター分析を行い比較しました。
k-umeyamaが正解率0.982、k-means++(0.918)、k-means(0.775)となり、k-umeyamaが、分類精度が高い結果となりました。
パーマペンギンデータセットを用いたクラスター分析結果
(左:k-means、中央:k-means++、右:k-umeyama)

*パーマペンギンデータセットは、南極のパーマー基地周辺のパーマー群島の島々で観察されたアデリー、ヒゲペンギン、ジェンツーペンギンの成鳥のサイズ測定、嘴の長さ (mm)、 嘴の深さ (mm)、フリッパーの長さ (mm)、体重 (g)などのデータが含まれています。データはKristen Gorman博士とパーマー基地長期生態学研究(LTER)プログラムによって収集されたものを利用しています。
Horst, A. M., Hill, A. P., & Gorman, K. B. (2020). palmerpenguins: Palmer Archipelago (Antarctica) penguin data. R package version 0.1.0. https://allisonhorst.github.io/palmerpenguins/. doi:10.5281/zenodo.3960218
精度テスト② 生活者のライフスタイルに関するアンケートデータを用いた分類
k-umeyamaとk-meansとを比較するために、「CORE(生活者総合ライフスタイル調査)」の食生活など生活分野の力の入れ具合を項目とするクラスター分析を行いました。
調査概要
| 調査地域 | 首都圏40Km圏 | ||||||||||||||||
| 調査対象とサンプル数 |
有効回収:3,000サンプル
|
||||||||||||||||
| サンプリング手法 | 市区町村人口に基づく確率比例抽出で200点を抽出し、住宅地図を用いてエリアサンプリング | ||||||||||||||||
| 調査手法 | 訪問・郵送併用の自記入式留置調査 | ||||||||||||||||
| 調査時期 | 2022年10月 | ||||||||||||||||
| 出典 | 生活者総合ライフスタイル調査CORE(株)クロス・マーケティング |
設問項目
| 生活の各分野に、あなたはどの程度力を入れてますか | 選択肢 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
比較のフローとしては、アンケート調査のベースデータについて、k-meansでは14変数の因子分析、直交化を行い、3因子の因子得点を用いています。k-umeyamaは、現データをそのまま4クラスターで分析を行ない、精度検証をしました。
フリードマン・ルービン基準では、k-umeyamaが7.05、k-meansは5.27となりました。数値の大きい方がよいので、k-umeyamaの方が、精度がよいことになります。また、多変量分散分析(ウィルクスのラムダ、ピライのトレース、ホテリング・ローリーのトレース)でもk-umeyamaが優位な結果となりました。
CORE(生活者総合ライフスタイル調査)精度検証(k-meansとk-umeyamaの比較)
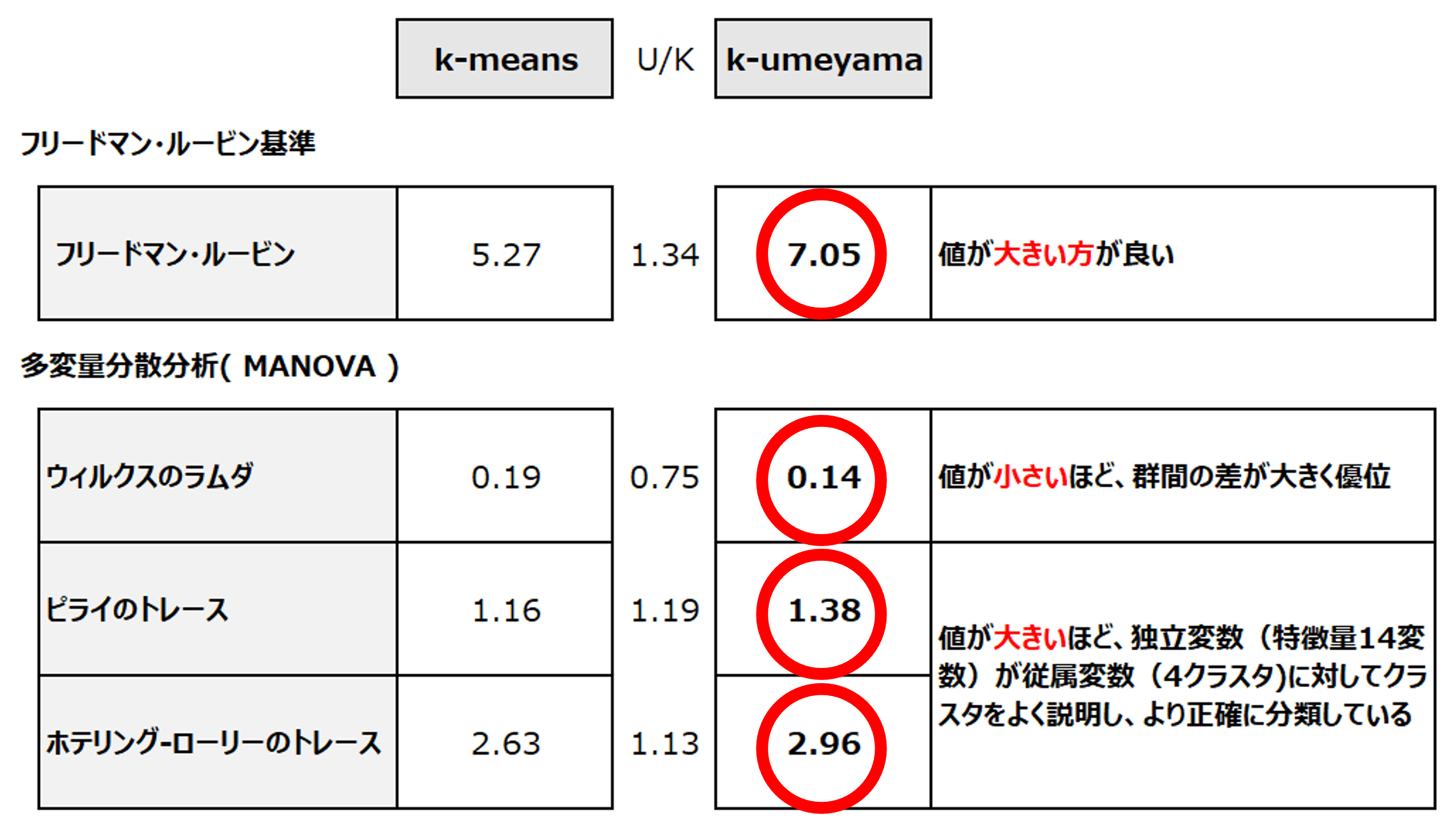
- フリードマン・ルービン:この基準は、クラスター間の分散が最大化され、クラスター内の分散が最小化されるようなグループ分けを評価するものです。具体的には、クラスター内のサンプル間の距離(つまりクラスタ内の分散)が小さいことと、異なるクラスター間のサンプル間の距離(つまりクラスタ間の分散)が大きいことが、良いクラスタリングの指標として用いられます。この基準の値が大きい場合、それはクラスター間の分散が大きく、クラスター内の分散が小さいことを意味します。これは、各クラスターが互いによくクラスターいることを示唆しています。
- ウィルクスのラムダは、複数の群間(between-groups)と群内(within-groups)の変動を比較するための指標として導入されました。その値は0から1の範囲を取り、小さい値は群間の変動が大きく、群内の変動が小さいことを示します。これは、データが群ごとによく区別されていることを意味します。ウィルクスのラムダの小さい値は、クラスター(または群)内の距離が小さく、クラスター間の距離が大きいことを示唆します。
-
クラスター分析の結果に対して、ピライのトレースやホテリング・ローリーのトレースを用いることで、クラスター間の変動とクラスター内の変動を評価することができます。具体的には、これらの指標はクラスター間での従属変数の平均の違いを捉えるものとして使用されます。
ピライのトレースは、各従属変数に対しての群間と群内の分散の比率を合計したものであり、ホテリング・ローリーのトレースは、この比率の加重平均として計算されます。これらの指標が大きい場合、クラスター間の変動が大きく、各クラスターが良く区別されていることを示唆します。逆に、これらの指標が小さい場合、クラスター間の変動が小さく、クラスターの区別があまり明確でないことを示します。
以下の表は、k-umeyamaとk-meansそれぞれについて、各生活分野項目で集計したものです。
CORE(生活者総合ライフスタイル調査)のクラスター分析結果比較(左:k-means、右:k-umeyama)
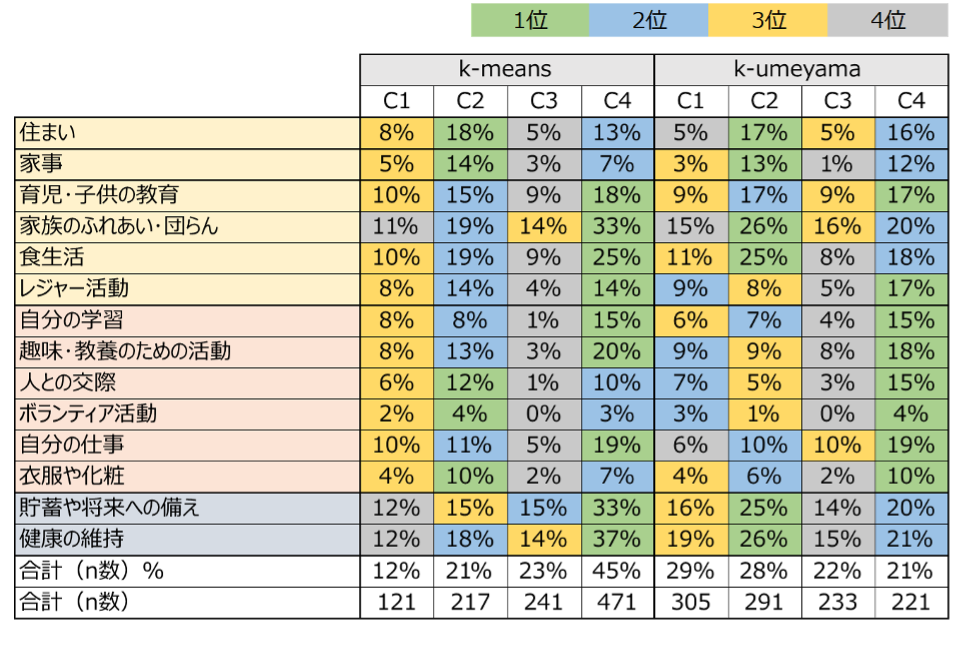
クラスター1(C1)~クラスター4(C4)は、各手法で生成された4つのクラスターを示しており、表示されるパーセントは、全サンプル数1,050人中、特定の生活分野に注力している人々の割合を示しています。また、色のグラデーション(緑→青→黄→グレー)は、1位から4位までの順位を示しています。
k-meansを使用した場合、クラスター1では主に3位が集中しており、クラスター2では住居、食事、交際、衣服・化粧に注力しています。クラスター3では、多くの生活分野で4位が集中しているものの、貯蓄だけは2位となっています。一方、クラスター4は全体の45%を占めており、多くの生活分野に注力していることが確認できます。
対照的に、k-umeyamaを使用した場合、クラスター1では2位と3位が多く、レジャーや趣味、交際などに注力しており、全体的にバランスが良いと言えます。クラスター2では、衣食住や貯蓄に注力し、家族や健康にも力を入れているが、レジャー活動は控えめです。クラスター3では、4位が多く、生活全般で注力している分野が少ないことが特徴で、住まい、家族、仕事などの基本的なものが3位となっています。そして、クラスター4では、仕事、趣味・教養、レジャー、育児に注力していることがわかります。
総じて、k-meansでは、クラスター間で生活分野への注力が段階的になっている印象を受けます。しかし、k-umeyamaでは、各クラスターが独自の特性を持ち、より明確に分類されました。クラスター分析の主要な目的は、データ間の関係性を正確に評価しつつ、各集団の特性を明確に捉えることです。このような背景から、k-umeyamaの採用により、消費者の実際のニーズや特性をより深く理解することができると期待できます。
非階層型クラスター分析手法の違い
改めて、クラスター分析における非階層クラスター分析手法のレビューを行うと、大きくは以下の4種類があげられます。
まず、k-meansはマックイーンによって提唱され、初期シードをユーザーが任意に指定したクラスター数を一括で選択して、クラスターの中心とサンプルの距離をユークリッド距離で測るものです。この場合、各クラスター間の分散共分散行列を利用しないで算出しています。つまり、相関性を考慮しないで、クラスター分析を行なっていることになります。
続いて、ダンのファジークラスタリングで、逆数を使うことで、サンプルが複数のクラスターにある程度の確率や度合いで所属することが可能となります。この所属の度合いをメンバーシップ値として表現しています。
セリオリはこのなかでは、唯一マハラノビスの汎距離を提案しています。この場合は、各クラスターの分散共分散は異なります。4番目はアーサーのk-means++というもので、初期シードを一つ一つ選んでいくものです。k-umeyamaの位置付けを見てみますと、初期シード選択にシグモイド関数と、クラスター間とサンプルの距離の測定に汎距離を利用することにより、クラスター分析の精度の向上につながったと考えられます。
今後も私たちは、データサイエンスのフィールドにおけるクラスタリング技術のさらなる発展に向けて研究を進めてまいります。
非階層クラスター分析の距離(左:k-means、中央:k-means++、右:k-umeyama)
| 発表 | 名称 | 初期シードの選択 | クラスター中心と サンプルの距離 |
各クラスターの分散共分散の利用 |
|---|---|---|---|---|
| MacQueen(1967) | k-means | 乱数で一括選択/ ユーザー指定 |
ユークリッド距離 | 利用せず |
| Dunn(1973) | FuzzyC-Means | 乱数で一括選択/ ユーザー指定 |
ユークリッド距離の逆数をメンバーシップ値に | 利用せず |
| Cerioli(2005) | 修正k-means | 提案なし | マハラノビス汎距離 | 異なる分散共分散行列を考慮 |
| Arthurら(2007) | k-means++ | 距離の2乗に比例した逐次選択 | ユークリッド距離 | 利用せず |
| 梅山(2023) | k-umeyama | Sigmoidによる逐次選択 | マハラノビス汎距離 | 異なる分散共分散行列を考慮 |
開発・研究協力:朝野熙彦 元東京都立大学教授 「マハラノビス研究会」の研究代表者
引用文献
- Arthur, D. and Vassilvitskii, S. (2007) k-means++: the advantages of careful seeding. SODA '07: Proceedings of the eighteenth annual ACM-SIAM symposium on discrete algorithms, 1027-1035 .
- Cerioli, A. (2005) K-means cluster analysis and Mahalanobis metrics: A problematic match or an overlooked opportunity?. Statistica Applicata, 17(1), 61-73.
- Friedman H.P. & J. Rubin (1967) On Some Invariant Criteria for Grouping Data, Journal of the American Statistical Association, 62:320, 1159-1178
- MacQueen, J.B. (1967) Some Methods for Classification and Analysis of Multivariate Observations. In: Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics, University of California Press, Berkeley, 281-297.
- Hotelling, H. (1936). Relations between two sets of variates. Biometrika, 28(3/4), 321-377.
- 水野欽司(1996)「多変量データ解析講義」朝倉書店
- Pillai, K. C. S. (1955). Some new test criteria in multivariate analysis. Annals of Mathematical Statistics, 26(1), 117-121.
- Wilks, S.S. (1932). Certain generalizations in the analysis of variance. Biometrika,24, 471–494.
資料のダウンロード
非階層クラスター(k-umeyama)の詳細資料、レポートはこちらからダウンロードいただけます。






























 を求める
を求める